Contenido
- 1 Métodos para Resolver Sistemas de Ecuaciones 3×3: Una Guía Detallada
- 2 ¿Cómo se resuelve un sistema de ecuaciones de 3×3?
- 3 ¿Cómo se resuelve un sistema de ecuaciones paso a paso?
- 4 ¿Cuántas soluciones tiene un sistema de ecuaciones lineales 3×3?
- 5 ¿Cómo podemos resolver los problemas con el sistema de ecuaciones?
- 6 Preguntas Frecuentes
- 6.1 ¿Qué métodos existen para resolver sistemas de ecuaciones 3×3?
- 6.2 ¿Cómo se aplica el método de sustitución en un sistema de ecuaciones 3×3?
- 6.3 ¿Cuándo es conveniente utilizar el método de matrices para resolver un sistema de ecuaciones 3×3?
- 6.4 ¿Cómo se verifica la solución de un sistema de ecuaciones 3×3?
Los sistemas de ecuaciones 3×3 son una herramienta fundamental en el ámbito de las matemáticas, utilizados para resolver problemas que involucran tres variables.
Estos sistemas pueden parecer complicados a primera vista, pero con el enfoque adecuado, se pueden abordar de manera efectiva. En este artículo, te guiaremos a través de un proceso paso a paso para resolver estos sistemas de ecuaciones.
Exploraremos diferentes métodos, como la sustitución, la eliminación y la regla de Cramer, y te proporcionaremos ejemplos prácticos para que puedas aplicar estos conocimientos en tus propios problemas.
Métodos para Resolver Sistemas de Ecuaciones 3×3: Una Guía Detallada
1. Método de Sustitución
El método de sustitución consiste en despejar una de las variables en una de las ecuaciones y sustituirla en las otras dos, de manera que se reduzca el sistema a uno de 2×2. Este proceso se repite hasta obtener el valor de todas las variables. Este método es especialmente útil cuando es fácil despejar una de las variables.
2. Método de Reducción
El método de reducción implica multiplicar una o más de las ecuaciones por constantes adecuadas de tal manera que, al sumarlas, una de las variables se cancele. Esto simplifica el sistema a uno de 2×2, que luego se resuelve por medio de sustitución o reducción nuevamente. Este método es efectivo cuando las ecuaciones tienen coeficientes que permiten la cancelación fácil de una variable.
3. Método de Matrices
El método de matrices utiliza operaciones matriciales para resolver el sistema de ecuaciones. Primero, se representa el sistema en forma matricial AX = B, donde A es la matriz de coeficientes, X es la matriz de variables y B es la matriz de términos constantes. Luego, se puede resolver utilizando la inversa de la matriz A (si existe) o mediante la regla de Cramer.
4. Método Gráfico
El método gráfico consiste en representar cada ecuación como un plano en el espacio tridimensional. La solución del sistema es el punto donde los tres planos se intersectan. Aunque este método proporciona una visualización del problema, es menos preciso y práctico para obtener soluciones exactas en sistemas 3×3.
5. Método de Eliminación de Gauss
El método de eliminación de Gauss es un procedimiento sistemático que utiliza operaciones elementales de fila para transformar la matriz aumentada del sistema en una matriz escalonada, de la cual se puede obtener la solución por sustitución regresiva. Este método es muy eficiente y se utiliza ampliamente en computación.
| Método | Descripción | Ventajas |
|---|---|---|
| Sustitución | Despeja variables y sustituye en otras ecuaciones. | Fácil de aplicar si una variable se despeja fácilmente. |
| Reducción | Multiplica ecuaciones y suma para cancelar variables. | Útil cuando los coeficientes permiten cancelación fácil. |
| Matrices | Utiliza operaciones matriciales para resolver el sistema. | Efectivo y sistemático, especialmente en computación. |
| Gráfico | Representa las ecuaciones como planos en 3D. | Proporciona visualización, pero menos preciso. |
| Eliminación de Gauss | Usa operaciones de fila para escalonar la matriz. | Muy eficiente y ampliamente utilizado en computación. |
¿Cómo se resuelve un sistema de ecuaciones de 3×3?

Método de sustitución
El método de sustitución consiste en despejar una variable en una de las ecuaciones y sustituirla en las otras dos ecuaciones, de modo que se reduzca el sistema a un sistema de dos ecuaciones con dos variables. A continuación, se resuelve este sistema de dos ecuaciones y se sustituyen los valores obtenidos en la ecuación original para encontrar el valor de la tercera variable.
- Despeja una variable de una de las ecuaciones. Por ejemplo, despeja x en la primera ecuación.
- Sustituye este valor de x en las otras dos ecuaciones.
- Resuelve el sistema de dos ecuaciones con dos variables que resulta.
- Sustituye los valores obtenidos en la ecuación original para encontrar el valor de la tercera variable.
Método de eliminación
El método de eliminación consiste en eliminar una variable sumando o restando las ecuaciones de manera adecuada. Se elige una variable para eliminar y se manipulan las ecuaciones para que los coeficientes de esa variable sean iguales y opuestos. Luego, se suman o restan las ecuaciones para eliminar esa variable y se obtiene un sistema de dos ecuaciones con dos variables.
- Elige una variable para eliminar. Por ejemplo, elige y.
- Manipula las ecuaciones de modo que los coeficientes de y sean iguales y opuestos en dos de las ecuaciones.
- Suma o resta estas ecuaciones para eliminar y.
- Repite el proceso para eliminar z.
- Resuelve la ecuación resultante para encontrar el valor de x.
- Sustituye este valor en las ecuaciones anteriores para encontrar los valores de y y z.
Método de matrices
El método de matrices utiliza operaciones matriciales para resolver el sistema de ecuaciones. Se escribe el sistema en forma matricial AX = B, donde A es la matriz de coeficientes, X es la matriz de variables y B es la matriz de términos independientes. Luego, se calcula la inversa de A y se multiplica por B para obtener la matriz de soluciones X.
- Escribe el sistema en forma matricial AX = B.
- Calcula la inversa de la matriz A. Si no existe, el sistema no tiene solución única.
- Multiplica la inversa de A por B para obtener la matriz de soluciones X.
¿Cómo se resuelve un sistema de ecuaciones paso a paso?
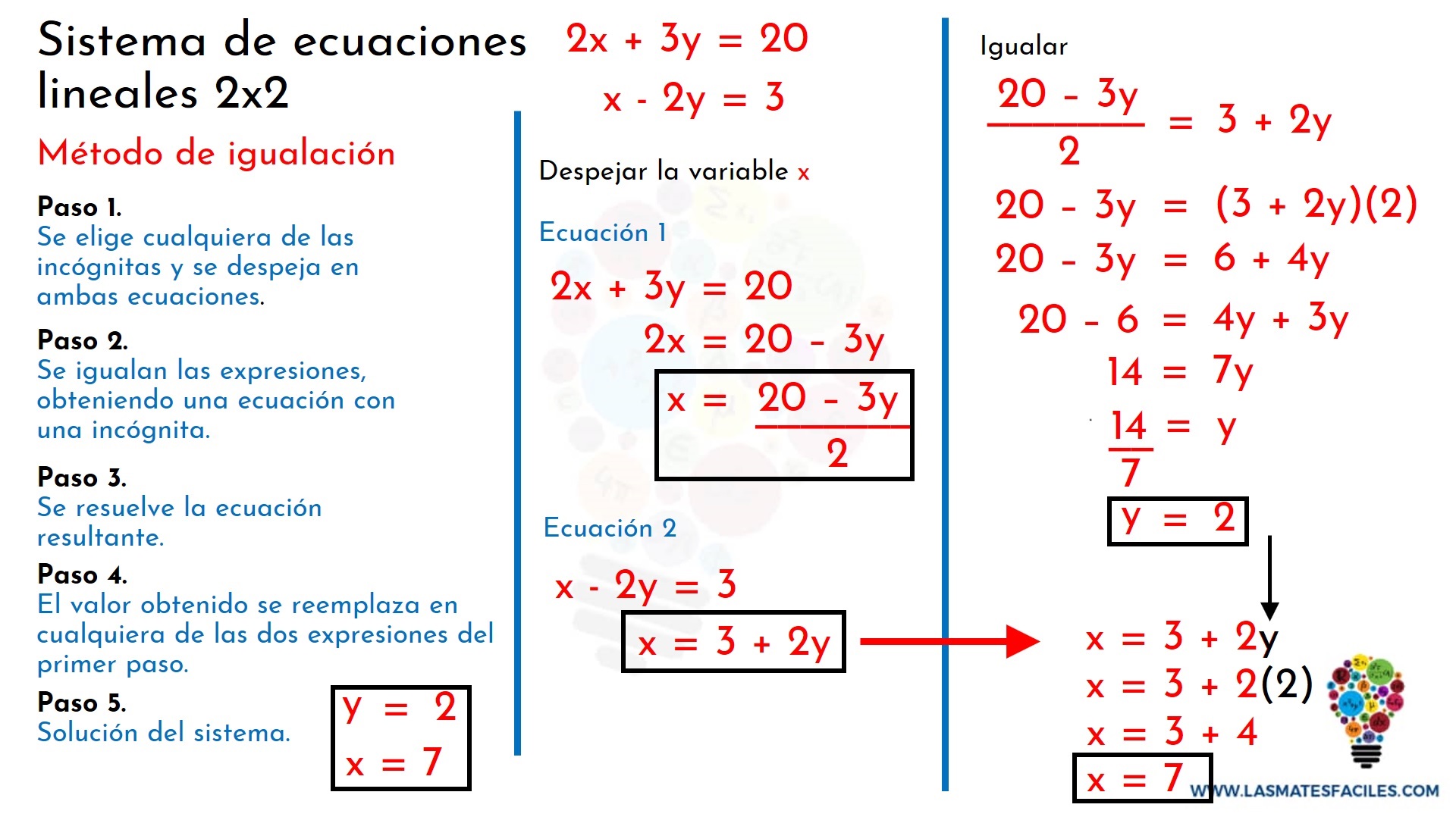
Definición de un sistema de ecuaciones
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que involucran dos o más variables. La solución de un sistema de ecuaciones es el conjunto de valores de las variables que satisfacen simultáneamente todas las ecuaciones del sistema. Para resolver un sistema de ecuaciones, existen varios métodos, entre los más comunes se encuentran el método de sustitución, el método de eliminación y el método gráfico.
Paso a paso: Método de Sustitución
El método de sustitución consiste en despejar una de las variables en una de las ecuaciones y sustituirla en la otra. A continuación, se resuelve la ecuación resultante y se encuentra el valor de la segunda variable. Finalmente, se sustituye el valor encontrado en cualquiera de las ecuaciones originales para hallar el valor de la primera variable. Este método es particularmente útil cuando una de las variables ya está despejada en una de las ecuaciones.
Paso a paso: Método de Eliminación
El método de eliminación consiste en manipular las ecuaciones de tal manera que, al sumarlas o restarlas, una de las variables se elimine. Una vez que se ha eliminado una variable, se resuelve la ecuación resultante para la variable restante. Luego, se sustituye este valor en una de las ecuaciones originales para encontrar el valor de la otra variable. Este método es particularmente útil cuando los coeficientes de una de las variables son los mismos o pueden hacerse los mismos mediante la multiplicación de una o ambas ecuaciones por un número adecuado.
¿Cuántas soluciones tiene un sistema de ecuaciones lineales 3×3?
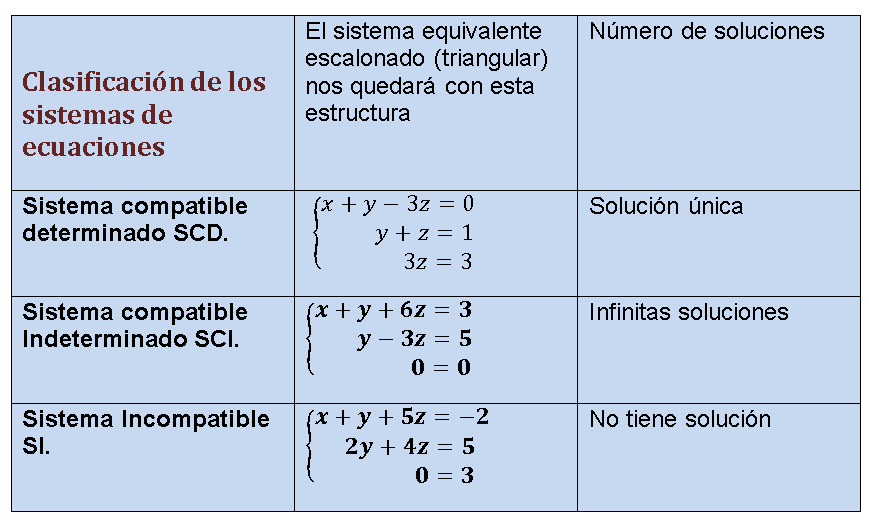
Un sistema de ecuaciones lineales 3×3 puede tener una solución única, infinitas soluciones o ninguna solución. Esto depende de la relación entre las ecuaciones y si estas son independientes o no.
Una solución única
Cuando un sistema de ecuaciones lineales 3×3 tiene una solución única, significa que las tres ecuaciones se intersectan en un único punto. Esto ocurre cuando las ecuaciones son independientes y no hay ninguna relación de dependencia entre ellas.
- Las ecuaciones representan tres planos que se intersectan en un solo punto.
- El sistema tiene una solución única si el determinante de la matriz de coeficientes no es cero.
- La solución puede ser encontrada utilizando métodos como la eliminación de Gauss, la regla de Cramer o la inversión de matrices.
Infinitas soluciones
Cuando un sistema de ecuaciones lineales 3×3 tiene infinitas soluciones, significa que las tres ecuaciones representan planos que se intersectan en una línea o que son coincidentes. Esto ocurre cuando hay una relación de dependencia entre las ecuaciones.
- Las ecuaciones representan tres planos que se intersectan en una línea.
- El sistema tiene infinitas soluciones si el determinante de la matriz de coeficientes es cero y al menos uno de los determinantes de las matrices de coeficientes ampliadas es cero.
- En este caso, la solución general se puede expresar en términos de uno o más parámetros.
Ninguna solución
Cuando un sistema de ecuaciones lineales 3×3 no tiene solución, significa que las ecuaciones representan planos que no se intersectan. Esto ocurre cuando hay una contradicción entre las ecuaciones.
- Las ecuaciones representan tres planos que no tienen puntos en común.
- El sistema no tiene solución si el determinante de la matriz de coeficientes es cero y todos los determinantes de las matrices de coeficientes ampliadas son diferentes de cero.
- En este caso, se dice que el sistema es inconsistente.
¿Cómo podemos resolver los problemas con el sistema de ecuaciones?

Métodos de Resolución de Sistemas de Ecuaciones
Existen varios métodos para resolver sistemas de ecuaciones, entre los que se destacan el método de sustitución, el de eliminación y el de igualación. Estos métodos permiten encontrar las soluciones o valores de las variables que satisfacen todas las ecuaciones del sistema.
- Sustitución: Se despeja una variable en una ecuación y se sustituye en la otra.
- Eliminación: Se suman o restan las ecuaciones para eliminar una variable y resolver la restante.
- Igualación: Se despeja la misma variable en ambas ecuaciones y luego se igualan para resolver la otra variable.
Aplicación de los Métodos en Problemas Prácticos
Para resolver los problemas con sistemas de ecuaciones, es crucial identificar claramente las variables y plantear correctamente las ecuaciones que representan la situación. Luego, se puede aplicar cualquiera de los métodos mencionados para encontrar las soluciones.
- Identificar variables: Reconocer las incógnitas del problema.
- Plantear ecuaciones: Establecer las relaciones entre las variables.
- Seleccionar método: Elegir el método más adecuado para resolver el sistema.
Importancia de la Práctica y la Comprensión Conceptual
La práctica constante y la comprensión sólida de los conceptos son fundamentales para resolver eficientemente los sistemas de ecuaciones. La familiaridad con los diferentes métodos, junto con la habilidad para interpretar los resultados, facilita la resolución de problemas complejos.
- Práctica regular: Resolver ejercicios variados para afianzar los conocimientos.
- Comprensión conceptual: Entender los principios detrás de cada método.
- Interpretación de resultados: Analizar y aplicar las soluciones encontradas.
Preguntas Frecuentes
¿Qué métodos existen para resolver sistemas de ecuaciones 3×3?
Existen varios métodos para resolver sistemas de ecuaciones 3×3, entre los más comunes se encuentran: método de sustitución, método de eliminación, método de igualación y método de matrices. Cada uno de estos métodos tiene sus propias ventajas y desventajas, y su elección depende de la complejidad de las ecuaciones y de las preferencias personales. El método de matrices, por ejemplo, es especialmente útil en sistemas de ecuaciones grandes y complejos, ya que permite una solución sistemática y ordenada.
¿Cómo se aplica el método de sustitución en un sistema de ecuaciones 3×3?
El método de sustitución en un sistema de ecuaciones 3×3 implica resolver una de las ecuaciones para una de las variables, y luego sustituir esa expresión en las otras dos ecuaciones para reducir el sistema a un sistema de dos ecuaciones con dos variables. Luego, se repite el proceso hasta obtener una sola ecuación con una variable. Una vez que se tiene la solución para esa variable, se puede sustituir hacia atrás para encontrar las otras variables. Este método es útil cuando una o más de las ecuaciones pueden ser fácilmente resueltas para una variable.
¿Cuándo es conveniente utilizar el método de matrices para resolver un sistema de ecuaciones 3×3?
El método de matrices es especialmente conveniente cuando se trata de sistemas de ecuaciones 3×3 que son complejos y difíciles de resolver por los métodos de sustitución o eliminación. Este método utiliza operaciones matriciales para resolver el sistema de ecuaciones. Implica la creación de una matriz de coeficientes y una matriz de constantes, y luego la aplicación de operaciones de matriz para llegar a una solución. Este método es sistemático y reduce la probabilidad de errores de cálculo.
¿Cómo se verifica la solución de un sistema de ecuaciones 3×3?
Una vez que se ha obtenido una solución para un sistema de ecuaciones 3×3, es importante verificar la solución para asegurarse de que es correcta. Esto se hace sustituyendo los valores obtenidos de las variables en cada una de las ecuaciones originales. Si los valores satisfacen todas las ecuaciones, entonces la solución es correcta. Si no, es necesario revisar los cálculos para encontrar y corregir cualquier error. Esta verificación es crucial para garantizar la precisión de la solución.


Deja una respuesta