Los trinomios cuadrados perfectos tienen propiedades únicas que los hacen más fáciles de factorizar y manipular en comparación con otros tipos de expresiones algebraicas. En esta publicación, exploraremos en detalle qué son los trinomios cuadrados perfectos, cómo identificarlos, factorizarlos utilizando fórmulas específicas y resolver algunos ejercicios prácticos.
Contenido
¿Qué es un trinomio cuadrado perfecto?
Un cuadrado perfecto es un número que resulta de multiplicar un número por sí mismo. Por ejemplo, 9 es un cuadrado perfecto porque ![]() . En términos algebraicos, un cuadrado perfecto es una expresión de la forma
. En términos algebraicos, un cuadrado perfecto es una expresión de la forma ![]() , donde
, donde ![]() es un número o una variable.
es un número o una variable.
Con esta comprensión previa…
Podemos definir un trinomio cuadrado perfecto como una expresión algebraica que puede ser factorizada como el cuadrado de un binomio. Es decir, un trinomio cuadrado perfecto es una expresión de la forma ![]() , donde
, donde ![]() y
y ![]() son términos que pueden ser variables o constantes. Esta forma particular de trinomio cuadrado perfecto surge de la aplicación de la identidad del cuadrado perfecto
son términos que pueden ser variables o constantes. Esta forma particular de trinomio cuadrado perfecto surge de la aplicación de la identidad del cuadrado perfecto ![]() .
.
En resumen, un trinomio cuadrado perfecto es una expresión algebraica que puede ser escrita como el cuadrado de un binomio, siguiendo la forma ![]() , donde
, donde ![]() y
y ![]() pueden ser términos variables o constantes. Este tipo de trinomio tiene propiedades especiales que facilitan su factorización y su identificación es fundamental en álgebra y cálculo.
pueden ser términos variables o constantes. Este tipo de trinomio tiene propiedades especiales que facilitan su factorización y su identificación es fundamental en álgebra y cálculo.
Cómo identificar un trinomio cuadrado perfecto
Identificar un trinomio como un trinomio cuadrado perfecto requiere comprender las características particulares que lo distinguen de otros trinomios. Aquí te explico cómo identificarlo de manera didáctica y detallada:
- Observa la estructura del trinomio: El primer paso para identificar un trinomio cuadrado perfecto es observar la estructura del trinomio en cuestión. Recuerda que un trinomio cuadrado perfecto sigue una forma específica:
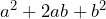 , donde
, donde 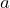 y
y 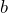 pueden ser términos variables o constantes.
pueden ser términos variables o constantes. - Verifica la presencia de tres términos: Un trinomio cuadrado perfecto siempre consta de tres términos. Estos términos pueden ser variables, constantes o una combinación de ambas. Es importante asegurarse de que el trinomio que estás analizando tenga exactamente tres términos.
- Comprueba si el primer y último término son cuadrados perfectos: El trinomio cuadrado perfecto tiene un primer término que es un cuadrado perfecto y un último término que también es un cuadrado perfecto. Por lo tanto, verifica si el primer término y el último término del trinomio pueden ser expresados como el cuadrado de un binomio. Por ejemplo,
 y
y  son cuadrados perfectos en el trinomio
son cuadrados perfectos en el trinomio  .
. - Revisa el término del medio: El término del medio en un trinomio cuadrado perfecto es dos veces el producto de las raíces cuadradas de los términos extremos. Es decir, el término del medio es el doble del producto de la raíz cuadrada del primer término y la raíz cuadrada del último término. Por ejemplo, en el trinomio
 , el término del medio es
, el término del medio es  , que es dos veces
, que es dos veces  .
.
Factorización de trinomios cuadrados perfectos
Una vez que has verificado que un trinomio es un trinomio cuadrado perfecto, el siguiente paso es factorizarlo, para ello hacemos usa de la fórmula del trinomio cuadrado perfecto:
Fórmula del trinomio cuadrado perfecto:
El trinomio cuadrado perfecto proviene del cuadrado de un binomio, que establece que el cuadrado de la o la diferencia de dos términos es igual al cuadrado del primer término más dos veces el producto de los dos términos más el cuadrado del segundo término. Entonces, la fórmula para factorizar el trinomio cuadrado perfecto es exactamente la misma pero desde la perspectiva contraria, es decir:
![]()
Donde a y b pueden representar constantes o variables, nota además que el signo del segundo término, determinará el signo que separa el binomio de la factorización.
Cómo factorizar un trinomio cuadrado perfecto:
Una vez que tenemos identificado que efectivamente se trata de un trinomio cuadrado perfecto, aplicamos el siguiente procedimiento para obtener la factorización de dicho trinomio;
Supongamos que tenemos el trinomio cuadrado perfecto ![]() . Queremos expresar este trinomio como el cuadrado de un binomio.
. Queremos expresar este trinomio como el cuadrado de un binomio.
- Identifica los términos cuadráticos y calcula sus raíces cuadradas: En primer lugar, identifica los términos cuadráticos en el trinomio. En el trinomio cuadrado perfecto
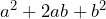 , los términos cuadráticos son
, los términos cuadráticos son  y
y  . En el caso del ejemplo los términos son
. En el caso del ejemplo los términos son  y
y  , debemos calcular las raíces de dichos términos para obtener entonces a y b, entonces en el ejemplo
, debemos calcular las raíces de dichos términos para obtener entonces a y b, entonces en el ejemplo  y
y  .
. - Observa el término del medio: Si ya verificaste que el trinomio es efectivamente un trinomio cuadrado perfecto, entonces sabes que el término del medio,
 , es dos veces el producto de
, es dos veces el producto de 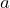 y
y 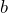 . Además de asegurarte de ello, deberás fijarte en su signo puesto que determinará el signo del binomio resultante. En el ejemplo, efectivamente el segundo término es
. Además de asegurarte de ello, deberás fijarte en su signo puesto que determinará el signo del binomio resultante. En el ejemplo, efectivamente el segundo término es  y tiene signo positivo
y tiene signo positivo - Aplica la fórmula y escribe la factorización: Utiliza la fórmula del trinomio cuadrado perfecto para factorizar el trinomio. La fórmula es
 . En el ejemplo tendríamos:
. En el ejemplo tendríamos: 
En la práctica, tanto el proceso de verificación como el de la factorización en sí, suelen hacerse en paralelo, por lo que un resumen del proceso de factorización sería:
- Identifica los términos cuadráticos y calcula sus raíces.
- Verifica que el segundo término cumple la condición
 e identifica su signo.
e identifica su signo. - Aplica la fórmula y factoriza.
Veamos a continuación una serie de ejercicios de factorización de trinomios cuadrados perfectos donde aplicamos el procedimiento descrito anteriormente.
Ejercicios de trinomio cuadrado perfecto ejemplos
Ejercicio 1. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() Si cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es positivo.
Si cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es positivo.
Paso 3: Escribimos el trinomio factorizado:
![]()
Ejercicio 2. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
. Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
Paso 3: Escribimos el trinomio factorizado:
![]()
Ejercicio 3. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
. Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
Paso 3: Escribimos el trinomio factorizado:
![]()
Ejercicio 4. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
. Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
Paso 3: Escribimos el trinomio factorizado:
![]()
Ejercicio 5. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es positivo.
. Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es positivo.
Paso 3: Escribimos el trinomio factorizado:
![]()
Ejercicio 6. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . No cumple la condición para ser un trinomio cuadrado perfecto.
. No cumple la condición para ser un trinomio cuadrado perfecto.
Paso 3: No es posible factorizar este trinomio como un cuadrado perfecto.
Ejercicio 7. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
. Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
Paso 3: Escribimos el trinomio factorizado:
![]()
Ejercicio 8. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
. Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
Paso 3: Escribimos el trinomio factorizado:
![]()
Ejercicio 9. ![]()
Solución
Paso 1: Identificamos los términos cuadráticos y calculamos sus raíces cuadradas:
![]()
![]()
Paso 2: Verificamos el segundo término para asegurarnos de que se trata de un trinomio cuadrado perfecto y establecemos el signo de dicho término:
![]() . Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
. Cumple la condición, por lo que se trata de un trinomio cuadrado perfecto y su signo es negativo.
![]()


Deja una respuesta