Polinomios: ¿Qué son?, elementos y tipos de polinomios

Los polinomios deben su origen a los Egipcios y Babilónicos aproximadamente 2000 años antes de Cristo, desarrollando este tema a través de los años.

En esta paginas encontraras todos lo relacionados al contenido de polinomio, desde definiciones, elementos, tipos, operaciones, factorizaciones, entre otros, esperando aclarar todas tus duras y colaborar en el desarrollo de tus tareas.

Contenido

1 ¿Qué es un polinomio?
2 Términos de un polinomio
3 Elementos de un polinomio
4 Clasificación o tipos de polinomios
5 Orden de un polinomio
6 Operaciones con polinomios.
7 Productos notables
8 Factorización de polinomios
9 Valor numérico de un polinomio
10 Raíz de un polinomio ó cero de un polinomio

¿Qué es un polinomio?

Se entiende por polinomio a la expresión algebraica conformada por un número finito de variables con exponentes enteros positivos y coeficientes, separados por operaciones aritméticas como la suma, resta y multiplicación.

Dentro de las diferentes definiciones nos encontramos también que:

Los polinomios son expresiones algebraicas conformadas por términos separados por operaciones de suma o resta.

Un ejemplo de polinomio sería:

$P(x)=x^{2}+2x^{4}-4x$

Términos de un polinomio

El termino de un polinomio es una expresión algebraica conformada por una variable, un exponente y un coeficiente.

Un ejemplo de término es:

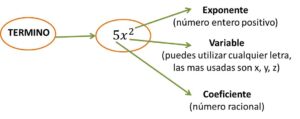
Los términos pueden ser semejantes en dos o mas polinomios cuando coinciden en la variable y el exponente independientemente que los coeficientes sean diferentes.

Si tenemos dos polinomios:

$P(x)=x^{2}+2x^{3}$

$Q(x)=4x^{2}+6x^{3}$

$x^{2}$ es semejante a $4x^{2}$

$2x^{3}$ es semejante a $6x^{3}$

Elementos de un polinomio

Los elementos de un polinomio son:

1.- Términos.

2.- Coeficientes: Son los números racionales que preceden a la variable.

3.- Término independiente: Es el termino donde el exponente de la variable vale cero. Dentro de la expresión algebraica se reconoce por que no posee variable. Por ejemplo en el polinomio;

$P(x)=x^{2}+2x^{7}+4$

el término independiente es el 4

4.- Grado de un polinomio: Lo determina el mayor exponente, siempre y cuando el coeficiente de dicho termino sea diferente a cero. ejemplo:

$P(x)=x^{2}+2x^{3}+4$

el polinomio tiene tres términos por tanto tiene tres exponentes (2,3,0) donde el mayor exponente es tres, por tanto es del tercer grado el polinomio.

Clasificación o tipos de polinomios

Existen muchas bibliográficas que diferencian a los polinomios como tipos y otros utilizan la palabra clasificación como un sinónimo, haciendo referencia al mismo contenido.

Los polinomios los podemos clasificar según:

1.- El número de términos los polinomios pueden ser:

Monomio: Polinomio formado por un solo termino.
Binomio: Polinomio formado por dos términos.
Trinomio: Polinomio formado por tres términos.

2.- Según el grado del polinomio puede ser:

Primer grado
Segundo grado
Tercer Grado
Cuarto grado
Quinto grado … dependiendo del mayor exponente, el mismo definirá el grado.

3.- Polinomios especiales:

Polinomios completos: Tiene todos los términos completos en la expresión, identificándose por la secuencia ascendente o descendente de sus exponente. Ejemplo:

$P(x)=x^{5}+2x^{4}+7x^{3}-5x^{2}+x-9$

si observamos tenemos los exponente 5,4,3,2,1 y 0, no falta ninguno en esa secuencia, por tanto el polinomio está completo.

Polinomios incompletos: En la expresión algebraica carece mínimo de un termino, identificándose por la ausencia de un exponente en la secuencia. Ejemplo:
$P(x)=x^{5}+2x^{4}+5x^{2}+x-9$
si observamos tenemos los exponente 5,4,2,1 y 0, faltaría el termino con exponente 3, por tanto el polinomio está incompleto.
Polinomio nulo: Se caracteriza por tener todos los coeficientes de sus términos iguales a cero. Ejemplo;

$P(x)=-9$

Polinomio multivariable: En sus términos se identifican dos o mas variables diferentes, ejemplo:

$P(x,y,z)=3x^{7}y-2zy^{9}+5xz-yz$

Es de acotar que la suma de los exponentes de cada variable que conforman a un termino, será el grado de dicho termino.

Orden de un polinomio

El orden de un polinomio es la forma de organizar los términos secuencialmente según el valor del exponente, facilitando muchas operaciones. El orden puede ser:

Ascendente: Los términos se agrupan del menor exponente al mayor exponente, independientemente que falte uno termino. Ejemplo:

$P(x)=3+x-2x^{2}-4x^{3}+5x^{4}+x^{5}$

Descendente: Los términos se agrupan del mayor exponente al menor exponente, independientemente que falte un termino. Ejemplo:

$P(x)=3x^{6}-2x^{5}-4x^{4}+5x^{3}+x^{2}-9x-3$

Pero tenemos el caso de polinomios con dos variables, para ordenarlos consideramos una de las variables según sea el interes al momento de trabajar con el polinomio, por ejemplo:

$P(x)=3+xy-2x^{2}y-4x^{3}y^{4}+5x^{4}y+x^{5}y^{6}$

si observamos el ejemplo el polinomio está ordenado de forma ascendente considerando la variable X.

Operaciones con polinomios.

Dentro de las operaciones con polinomios se encuentran:

Adición de polinomios

Se define adición de polinomios cuando se tiene dos o mas polinomios que dan como resultado a otro polinomio formado por la suma de los términos semejantes de los polinomios sumandos.

Diferencia o resta de polinomios

El proceso de restar dos o mas polinomios no es más que la suma del polinomio minuendo con el opuesto o simétrico del polinomio sustraendo.

Es de acotar que el opuesto de un polinomio se obtiene al cambiar el signo a todos los coeficiente.

Multiplicación de polinomios

El producto de dos polinomios es otro polinomio, cuyos términos se obtienen multiplicando cada termino de uno de los polinomios por cada uno de los términos del otro polinomio para finalmente reducir los términos semejantes.

División de polinomios

Para dividir polinomios partimos de entender la división de monomio como procedimiento básico. Esta división consiste primero se dividen los coeficientes entre si, aplicando la regla de los signos, posteriormente se divide las variable aplicando el cociente de potencia de igual base.

Para dividir un polinomio entre un monomio se aplica la regla de la propiedad distributiva de la suma respecto a la división.

Finalmente para dividir dos polinomios hay que acotar que solo es posible realizarla cuando el grado del polinomio dividiendo P(x) es mayor que el grado del polinomio divisor Q(x). El método utilizado para resolver este tipo de división se aplica el Método de Galera.

Productos notables

Se define como producto notable a los resultados del producto entre dos expresiones algebraicas, cuyas características se pueden generalizar a través de formulas especiales.

Entre los casos de productos notables que estudiaremos mas adelantes se encuentran:

Factorización de polinomios

Se define como factorización de un polinomio como un proceso mediante el cual un polinomio es expresado como producto de dos o mas polinomios, de grado menor o igual que el suyo denominado factores.

Dentro de las operaciones de factorización estudiaremos mas adelante:

Valor numérico de un polinomio

Se dice que el valor numérico de un polinomio P(x) para x=a lo denotamos como P(a), es el número resultante al sustituir el valor de X en el polinomio, efectuando las operaciones respectivas al caso.

Por ejemplo:

Encontrar el valor numérico del polinomio $P(x)= x^{2}+3x+4$ cuando x=2.

$P(x)= x^{2}+3x+4$

$P(2)= x^{2}+3x+4$

$P(2)= (2)^{2}+3(2)+4$

$P(2)= 4+6+4$

$P(2)= 16$

el valor numérico del polinomio $P(x)= x^{2}+3x+4$ cuando x=2 es 16.

Raíz de un polinomio ó cero de un polinomio

La raíz de un polinomio es llamada también como cero de un polinomio, dado que es el valor que asume X para que el polinomio de cero, en el enlace anterior podrás encontrar más detalles acerca de este tema con ejemplos que te permitirán aclarar el concepto fácilmente.