Contenido
- 1 Sistema de Ecuaciones Lineales con Dos Incógnitas: Un Enfoque Detallado
- 1.1 ¿Qué es un Sistema de Ecuaciones Lineales con Dos Incógnitas?
- 1.2 Métodos para Resolver un Sistema de Ecuaciones Lineales con Dos Incógnitas
- 1.3 Tipos de Soluciones en un Sistema de Ecuaciones Lineales con Dos Incógnitas
- 1.4 Aplicaciones de los Sistemas de Ecuaciones Lineales con Dos Incógnitas
- 1.5 Representación Matricial de un Sistema de Ecuaciones Lineales con Dos Incógnitas
- 2 ¿Cómo se resuelve una ecuación lineal con dos incógnitas?
- 3 ¿Qué son sistemas de ecuaciones lineales con dos incógnitas?
- 4 ¿Cuál es el sistema de ecuaciones lineales en dos variables?
- 5 ¿Qué es un sistema de dos ecuaciones y dos incógnitas compatibles y determinados?
- 6 Preguntas Frecuentes
- 6.1 ¿Qué es un sistema de ecuaciones lineales con dos incónitas?
- 6.2 ¿Cuáles son los métodos para resolver un sistema de ecuaciones lineales con dos incógnitas?
- 6.3 ¿Qué es el método gráfico para resolver un sistema de ecuaciones lineales con dos incógnitas?
- 6.4 ¿Qué significa cuando un sistema de ecuaciones lineales con dos incógnitas no tiene solución o tiene infinitas soluciones?
En el fascinante mundo de las matemáticas, los sistemas de ecuaciones lineales con dos incógnitas representan una herramienta fundamental para resolver problemas en diversas áreas del conocimiento. Estos sistemas, compuestos por dos ecuaciones lineales con dos variables, permiten hallar soluciones específicas que satisfacen ambas ecuaciones simultáneamente.
Mediante métodos algebraicos como la sustitución, la eliminación o la representación gráfica, es posible determinar los valores de las incógnitas que hacen verdaderas ambas igualdades. Son de gran utilidad en la física, la economía, la ingeniería y muchas otras disciplinas que requieren modelos matemáticos para analizar situaciones reales y tomar decisiones informadas.
Sistema de Ecuaciones Lineales con Dos Incógnitas: Un Enfoque Detallado
¿Qué es un Sistema de Ecuaciones Lineales con Dos Incógnitas?
Un sistema de ecuaciones lineales con dos incógnitas es un conjunto de dos ecuaciones lineales donde hay dos variables desconocidas, generalmente representadas como x e y.
El objetivo de resolver un sistema de ecuaciones lineales es encontrar los valores de estas incógnitas que satisfagan ambas ecuaciones simultáneamente. Estos sistemas son ampliamente utilizados en matemáticas, ciencias e ingeniería para modelar y resolver problemas que involucran relaciones lineales entre dos variables.
Métodos para Resolver un Sistema de Ecuaciones Lineales con Dos Incógnitas
Existen varios métodos para resolver un sistema de ecuaciones lineales con dos incógnitas, siendo los más comunes:
– Método de Sustitución: Consiste en despejar una de las variables en una de las ecuaciones y sustituirla en la otra ecuación para resolver la variable restante.
– Método de Igualación: Implica despejar la misma variable en ambas ecuaciones e igualarlas para resolver una de las incógnitas.
– Método Gráfico: Se basa en graficar ambas ecuaciones en un plano cartesiano; el punto de intersección de las rectas representa la solución del sistema.
– Método de Eliminación: Se suma o resta las ecuaciones para eliminar una de las variables y resolver la otra.
Tipos de Soluciones en un Sistema de Ecuaciones Lineales con Dos Incógnitas
Un sistema de ecuaciones lineales con dos incógnitas puede tener tres tipos de soluciones:
– Solución Única: Cuando las rectas se intersecan en un único punto, lo que significa que hay un par de valores de x e y que satisfacen ambas ecuaciones.
– Sin Solución: Cuando las rectas son paralelas y nunca se intersecan, lo que indica que no hay valores de x e y que cumplan con ambas ecuaciones simultáneamente.
– Infinitas Soluciones: Cuando las rectas son coincidentes, lo que significa que todos los puntos en una recta también están en la otra, resultando en infinitos pares de x e y que satisfacen el sistema.
Aplicaciones de los Sistemas de Ecuaciones Lineales con Dos Incógnitas
Los sistemas de ecuaciones lineales con dos incógnitas tienen numerosas aplicaciones prácticas en diversas disciplinas. Por ejemplo, en economía, pueden utilizarse para modelar la oferta y la demanda de productos.
En física, son útiles para calcular velocidades y distancias. En ingeniería, ayudan a diseñar y analizar estructuras y circuitos eléctricos. En química, se emplean para balancear ecuaciones químicas y calcular concentraciones.
Representación Matricial de un Sistema de Ecuaciones Lineales con Dos Incógnitas
Un sistema de ecuaciones lineales con dos incógnitas también puede representarse mediante matrices.
La forma general de un sistema de ecuaciones lineales en forma matricial es AX = B, donde A es la matriz de coeficientes, X es el vector de incógnitas y B es el vector de términos independientes. Esta representación facilita el uso de métodos matriciales y computacionales para resolver sistemas de ecuaciones, especialmente cuando hay múltiples incógnitas y ecuaciones.
| Método | Ventajas | Consideraciones |
|---|---|---|
| Método de Sustitución | Directo y fácil de aplicar para sistemas pequeños. | Puede volverse complejo con ecuaciones muy elaboradas. |
| Método de Igualación | Útil para sistemas con variables fácilmente despejables. | Requiere buen manejo algebraico. |
| Método Gráfico | Proporciona una visualización del sistema. | Menos preciso para determinar soluciones exactas. |
| Método de Eliminación | Efectivo para eliminar variables y simplificar el sistema. | Requiere un buen entendimiento de operaciones con ecuaciones. |
¿Cómo se resuelve una ecuación lineal con dos incógnitas?

Definición de ecuación lineal con dos incógnitas
Una ecuación lineal con dos incógnitas es una igualdad matemática donde se relacionan dos variables o desconocidas (generalmente representadas por x e y) a través de coeficientes y términos constantes.
La forma general de una ecuación lineal con dos incógnitas es ax + by = c, donde a, b y c son números reales (con a y b diferentes de cero).
Resolución de una ecuación lineal con dos incógnitas
- Representar la ecuación en su forma general: Escribir la ecuación de manera que esté en la forma general ax + by = c.
- Despejar una de las variables: Elegir una de las variables e despejarla en términos de la otra variable y los coeficientes.
- Asignar valores a una variable: Seleccionar varios valores para la variable que no se despejó y calcular los correspondientes valores para la variable despejada. Esto generará pares ordenados (x, y) que satisfacen la ecuación.
Interpretación gráfica de la solución
Cada par ordenado obtenido al resolver la ecuación lineal con dos incógnitas representa un punto en el plano cartesiano. Al unir estos puntos se forma una línea recta, que es la representación gráfica de la ecuación. Cualquier punto sobre esta línea es una solución de la ecuación, lo que significa que hay infinitas soluciones para una ecuación lineal con dos incógnitas.
¿Qué son sistemas de ecuaciones lineales con dos incógnitas?
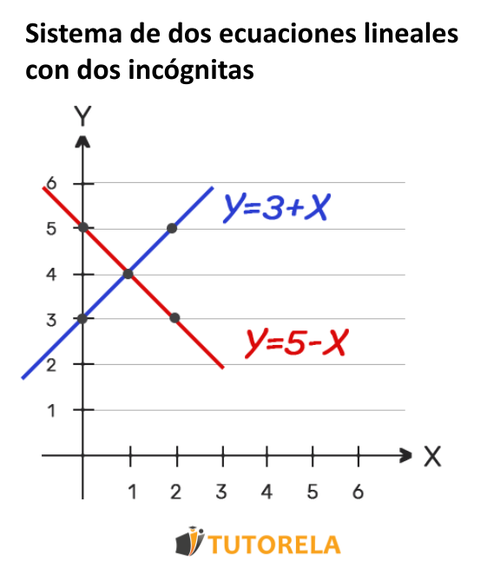
Los sistemas de ecuaciones lineales con dos incógnitas son un conjunto de dos o más ecuaciones lineales donde se busca encontrar los valores de dos variables, generalmente denominadas como x e y. Estos sistemas se utilizan en diversas áreas, como en la física, economía e ingeniería, para modelar y resolver problemas que involucren relaciones lineales entre dos variables.
Métodos de resolución de sistemas de ecuaciones lineales con dos incógnitas
Los sistemas de ecuaciones lineales con dos incógnitas pueden resolverse mediante diferentes métodos, entre los que se destacan:
- Método gráfico: Consiste en representar las ecuaciones en el plano cartesiano y encontrar el punto de intersección entre las rectas, el cual corresponde a la solución del sistema.
- Método de sustitución: Se despeja una de las variables en una de las ecuaciones y se sustituye en la otra, obteniendo así una ecuación con una sola variable, la cual se resuelve y se vuelve a sustituir para encontrar el valor de la otra variable.
- Método de igualación: Se despeja la misma variable en ambas ecuaciones y se igualan las expresiones resultantes, obteniendo una ecuación con una sola variable, la cual se resuelve y se sustituye para encontrar el valor de la otra variable.
Tipos de soluciones en sistemas de ecuaciones lineales con dos incógnitas
Los sistemas de ecuaciones lineales con dos incógnitas pueden tener diferentes tipos de soluciones:
- Solución única: Cuando las rectas representadas por las ecuaciones se intersectan en un único punto, el sistema tiene una solución única.
- Solución infinita: Cuando las rectas representadas por las ecuaciones son coincidentes, es decir, son la misma recta, el sistema tiene infinitas soluciones.
- Sin solución: Cuando las rectas representadas por las ecuaciones son paralelas y nunca se intersectan, el sistema no tiene solución.
Aplicaciones de los sistemas de ecuaciones lineales con dos incógnitas
Los sistemas de ecuaciones lineales con dos incógnitas tienen varias aplicaciones en la vida real y en diversas áreas del conocimiento:
- Problemas de mezclas: Se utilizan para calcular la cantidad de ingredientes necesarios en una mezcla, como en la elaboración de aleaciones o en la dilución de líquidos.
- Problemas de economía: Se emplean en la modelización de situaciones económicas, como la relación entre la oferta y la demanda, o el cálculo de costos y beneficios.
- Problemas de física: Se aplican en la resolución de problemas que involucran fuerzas, velocidades o movimientos, como en el cálculo de la trayectoria de un proyectil o en el equilibrio de fuerzas.
¿Cuál es el sistema de ecuaciones lineales en dos variables?

Un sistema de ecuaciones lineales en dos variables es un conjunto de dos o más ecuaciones lineales con dos variables. Estas ecuaciones se representan generalmente como ax + by = c y dx + ey = f, donde a, b, c, d, e y f son constantes y x e y son las variables. La solución a un sistema de ecuaciones lineales es el par de valores (x, y) que satisfacen ambas ecuaciones simultáneamente.
Formas de representar un sistema de ecuaciones lineales
Un sistema de ecuaciones lineales en dos variables se puede representar de varias maneras:
- Forma estándar: Ax + By = C, donde A, B y C son números reales y A y B no son ambos cero.
- Forma de pendiente-intersección: y = mx + b, donde m es la pendiente de la recta y b es la intersección con el eje y.
- Forma punto-pendiente: y – y1 = m(x – x1), donde m es la pendiente de la recta y (x1, y1) es un punto en la recta.
Métodos para resolver un sistema de ecuaciones lineales
Hay varios métodos para resolver un sistema de ecuaciones lineales en dos variables:
- Método de sustitución: Se resuelve una de las ecuaciones para una variable y luego se sustituye ese valor en la otra ecuación para encontrar el valor de la segunda variable.
- Método de eliminación: Se multiplican las ecuaciones por factores que hacen que los coeficientes de una de las variables sean iguales, luego se suman o restan las ecuaciones para eliminar una variable y resolver para la otra.
- Método gráfico: Se grafican ambas ecuaciones en el mismo plano coordenado y se encuentra el punto de intersección de las rectas, que representa la solución del sistema.
Tipo de soluciones de un sistema de ecuaciones lineales
Un sistema de ecuaciones lineales en dos variables puede tener diferentes tipos de soluciones:
- Solución única: Cuando las rectas se intersectan en un solo punto, el sistema tiene una solución única.
- Solución infinita: Cuando las rectas son coincidentes (iguales), el sistema tiene infinitas soluciones.
- Sin solución: Cuando las rectas son paralelas y nunca se intersectan, el sistema no tiene solución.
¿Qué es un sistema de dos ecuaciones y dos incógnitas compatibles y determinados?

Un sistema de dos ecuaciones y dos incógnitas es un conjunto de dos ecuaciones lineales con dos variables (incógnitas) que se resuelven de manera simultánea. Cuando un sistema es compatible y determinado, significa que tiene una única solución, es decir, existe un par de valores para las variables que satisfacen ambas ecuaciones.
Condición para que un sistema sea compatible y determinado
Un sistema de dos ecuaciones y dos incógnitas es compatible y determinado si el determinante formado por los coeficientes de las variables es diferente de cero. Esto se puede representar como:
- Si tenemos un sistema de la forma:
a1 x + b1 y = c1
a2 x + b2 y = c2 - El determinante del sistema es:
det = a1 b2 – a2 b1 - Si det ≠ 0, entonces el sistema es compatible y determinado, y tiene una única solución.
Métodos de resolución
Existen diversos métodos para resolver un sistema de dos ecuaciones con dos incógnitas cuando es compatible y determinado:
- Método de sustitución: Consiste en despejar una de las variables en una de las ecuaciones y luego sustituirla en la otra ecuación para obtener el valor de la segunda variable.
- Método de igualación: Consiste en despejar la misma variable en ambas ecuaciones e igualarlas para obtener el valor de la otra variable. Luego, se sustituye este valor en cualquiera de las dos ecuaciones originales para obtener el valor de la variable despejada.
- Método de eliminación: Consiste en multiplicar una o ambas ecuaciones por números adecuados de tal manera que, al sumar las ecuaciones, una de las variables se elimine. Luego, se resuelve la ecuación resultante para obtener el valor de la otra variable y se sustituye en alguna de las ecuaciones originales para encontrar el valor de la variable eliminada.
Importancia de los sistemas de ecuaciones
Los sistemas de dos ecuaciones y dos incógnitas son una herramienta fundamental en diversas áreas del conocimiento, como:
- En matemáticas, son un elemento básico en el estudio de los sistemas lineales y en la resolución de problemas que involucran dos variables relacionadas.
- En ciencias físicas y naturales, permiten modelar y resolver situaciones en las que hay dos magnitudes relacionadas por leyes o principios físicos y químicos.
- En ciencias económicas y administrativas, son utilizados para resolver problemas de optimización, asignación de recursos y toma de decisiones en situaciones en las que hay dos variables que dependen una de la otra.
Preguntas Frecuentes
¿Qué es un sistema de ecuaciones lineales con dos incónitas?
Un sistema de ecuaciones lineales con dos incógnitas es un conjunto de dos ecuaciones lineales que tienen dos variables o incógnitas. Estas ecuaciones se representan generalmente como ax + by = c y dx + ey = f, donde a, b, d y e son los coeficientes de las variables x e y, y c y f son constantes. La resolución de este tipo de sistemas permite encontrar los valores de las incógnitas que satisfacen ambas ecuaciones simultáneamente.
¿Cuáles son los métodos para resolver un sistema de ecuaciones lineales con dos incógnitas?
Existen varios métodos para resolver un sistema de ecuaciones lineales con dos incógnitas. Los más comunes son el método de sustitución, el método de igualación y el método de eliminación. En el método de sustitución, se despeja una de las variables en una de las ecuaciones y se sustituye en la otra. En el método de igualación, se despeja la misma variable en ambas ecuaciones y se igualan las expresiones resultantes. En el método de eliminación, se suman o restan las ecuaciones de manera que una de las variables se elimine.
¿Qué es el método gráfico para resolver un sistema de ecuaciones lineales con dos incógnitas?
El método gráfico para resolver un sistema de ecuaciones lineales con dos incógnitas consiste en representar cada ecuación como una recta en el plano cartesiano. La solución del sistema es el punto donde las dos rectas se intersectan. Para utilizar este método, se deben despejar ambas ecuaciones para una de las variables, preferiblemente y, de manera que queden en la forma y = mx + b, donde m es la pendiente y b es el intercepto. Este método es útil para visualizar la solución, pero puede no ser práctico cuando se requiere una solución exacta.
¿Qué significa cuando un sistema de ecuaciones lineales con dos incógnitas no tiene solución o tiene infinitas soluciones?
Cuando un sistema de ecuaciones lineales con dos incógnitas no tiene solución, significa que las ecuaciones representan dos rectas paralelas que nunca se intersectan. Esto ocurre cuando las rectas tienen la misma pendiente pero diferentes interceptos. Por otro lado, si un sistema de ecuaciones lineales tiene infinitas soluciones, significa que ambas ecuaciones representan la misma recta. Esto ocurre cuando las ecuaciones son múltiplos uno del otro. En ambos casos, no existe una única solución que satisfaga ambas ecuaciones.


Deja una respuesta