Contenido
Las ecuaciones de segundo grado son una parte fundamental en el estudio de las matemáticas, y su resolución mediante factorización es una de las técnicas más utilizadas.
Esta técnica nos permite descomponer una ecuación cuadrática en dos factores lineales, facilitando así su resolución. En el presente artículo, exploraremos en profundidad este método, analizando paso a paso cómo realizar la factorización de una ecuación de segundo grado, los posibles inconvenientes que pueden surgir durante el proceso y cómo superarlos, y finalmente, cómo interpretar y utilizar los resultados obtenidos.
Métodos de Factorización para Resolver Ecuaciones de Segundo Grado
Las ecuaciones de segundo grado son aquellas que tienen la forma general ax^2 + bx + c = 0, donde a, b y c son números reales y a ≠ 0. La factorización es una técnica útil para resolver este tipo de ecuaciones.
A continuación, se presentan cinco métodos comunes de factorización.
Factorización por Método de Prueba y Error
Este método implica buscar dos números que, al multiplicarse, den como resultado el término cuadrático (ax^2) y, al sumarse, den como resultado el término lineal (bx).
Por ejemplo, para factorizar la ecuación x^2 + 5x + 6 = 0, buscamos dos números que multiplicados den 6 y sumados den 5. Estos números son 2 y 3, por lo que la ecuación se factoriza como (x + 2)(x + 3) = 0.
Factorización por Método de la Diferencia de Cuadrados
Este método se utiliza cuando la ecuación tiene la forma ax^2 – c = 0. Se factoriza como (√ax – √c)(√ax + √c) = 0. Por ejemplo, la ecuación x^2 – 9 = 0 se factoriza como (x – 3)(x + 3) = 0.
Factorización por Método de Factor Común
Cuando todos los términos de la ecuación tienen un factor común, se puede factorizar sacando este factor común.
Por ejemplo, en la ecuación 2x^2 + 6x + 4 = 0, el factor común es 2. Sacando este factor, la ecuación se factoriza como 2(x^2 + 3x + 2) = 0, y posteriormente como 2(x + 1)(x + 2) = 0.
Factorización por Método de Agrupamiento
Este método se utiliza cuando no hay un factor común en todos los términos, pero sí en grupos de términos.
Por ejemplo, en la ecuación x^2 + 2x – 3x – 6 = 0, se pueden agrupar los términos como (x^2 + 2x) + (-3x – 6) = 0. Luego, se factoriza cada grupo: x(x + 2) – 3(x + 2) = 0. Finalmente, se factoriza el término común (x + 2): (x – 3)(x + 2) = 0.
Factorización por Método de Completar el Cuadrado
Este método implica transformar la ecuación original a una forma (x + p)^2 = q.
Por ejemplo, para la ecuación x^2 + 6x + 5 = 0, se añade y se resta el término (6/2)^2 = 9 para completar el cuadrado: x^2 + 6x + 9 – 9 + 5 = 0. Esto se simplifica a (x + 3)^2 – 4 = 0, lo que nos da la factorización (x + 3 + 2)(x + 3 – 2) = (x + 5)(x + 1) = 0.
| Método de Factorización | Descripción |
|---|---|
| Prueba y Error | Se busca dos números que, al multiplicarse, den el término cuadrático y, al sumarse, den el término lineal. |
| Diferencia de Cuadrados | Se aplica cuando la ecuación es de la forma ax^2 – c = 0. |
| Factor Común | Se utiliza cuando todos los términos tienen un factor común. |
| Agrupamiento | Se usa cuando no hay un factor común en todos los términos, pero sí en grupos de términos. |
| Completar el Cuadrado | Implica transformar la ecuación a una forma (x + p)^2 = q. |
¿Qué son las ecuaciones de segundo grado por factorización?

Las ecuaciones de segundo grado por factorización son una herramienta matemática utilizada para resolver ecuaciones cuadráticas.
La factorización es el proceso de descomponer una ecuación en factores más simples. Estos factores son multiplicados para obtener la ecuación original.
La factorización es una de las formas más comunes de resolver ecuaciones cuadráticas, que tienen la forma general ax^2 + bx + c = 0, donde a, b, y c son números reales y a ≠ 0.
Proceso de factorización
El proceso de factorización implica identificar los factores que, al ser multiplicados, dan como resultado la ecuación original. Para hacer esto, se siguen varios pasos:
- Identificar los términos a, b y c de la ecuación cuadrática.
- Encontrar dos números cuya suma sea igual a b y cuyo producto sea igual a ac.
- Reescribir la ecuación con estos dos números.
- Factorizar por grupos.
Resolución de ecuaciones factorizadas
Una vez que la ecuación ha sido factorizada, se puede resolver fácilmente.
- Una vez factorizada, la ecuación se convierte en un producto de dos factores igual a cero.
- Se aplica la propiedad de que si un producto es igual a cero, entonces uno o ambos factores deben ser cero.
- Se resuelve para cada factor igualado a cero para encontrar las soluciones de la ecuación cuadrática.
Importancia de la factorización
La factorización es una herramienta valiosa en matemáticas porque:
- Permite resolver ecuaciones cuadráticas de manera más simple y directa en muchos casos.
- Ayuda a simplificar expresiones algebraicas, haciendo más fácil la manipulación y el análisis de estas.
- Puede revelar propiedades importantes de las ecuaciones, como sus raíces o soluciones.
¿Cómo factorizar una ecuación?

Factorizar una ecuación es el proceso de descomponer un polinomio en el producto de dos o más factores. Esto es útil para simplificar expresiones algebraicas y resolver ecuaciones. A continuación, se presentan tres métodos comunes para factorizar ecuaciones:
Método de Factor Común
El método de factor común implica encontrar un factor que sea común a todos los términos de la ecuación. Esto se hace siguiendo estos pasos:
- Identificar el factor común en todos los términos.
- Dividir cada término por el factor común.
- Escribir la ecuación como el producto del factor común y la expresión resultante de la división.
Diferencia de Cuadrados
Este método se utiliza cuando la ecuación es una diferencia de dos cuadrados perfectos. Los pasos son:
- Identificar que la ecuación es de la forma a^2 – b^2.
- Factorizar la ecuación como (a + b)(a – b).
Trinomio Cuadrado Perfecto
Este método se utiliza cuando la ecuación es un trinomio cuadrado perfecto. Los pasos son:
- Identificar que la ecuación es de la forma a^2 + 2ab + b^2 o a^2 – 2ab + b^2.
- Factorizar la ecuación como (a + b)^2 si es de la forma a^2 + 2ab + b^2, o como (a – b)^2 si es de la forma a^2 – 2ab + b^2.
¿Qué es una ecuación factorizada?

Una ecuación factorizada es una ecuación algebraica que se expresa como el producto de dos o más factores. Estos factores pueden ser números, variables o expresiones algebraicas. La factorización es un proceso que permite descomponer una ecuación en sus factores constituyentes, lo cual facilita su resolución y simplificación.
Proceso de factorización
El proceso de factorización implica identificar los factores comunes en una ecuación y expresarla como el producto de estos factores. Esto se puede realizar mediante varias técnicas, como:
- Factor común: Se busca el factor que es común a todos los términos de la ecuación y se factoriza.
- Diferencia de cuadrados: Se aplica cuando la ecuación es una resta de dos expresiones al cuadrado.
- Trinomio cuadrado perfecto: Se utiliza cuando la ecuación es un trinomio que es el cuadrado de un binomio.
Ventajas de la factorización
La factorización de ecuaciones ofrece varias ventajas en el ámbito del álgebra, como:
- Facilita la simplificación de expresiones algebraicas complejas.
- Permite resolver ecuaciones de manera más rápida y sencilla.
- Ayuda a entender mejor la estructura y las propiedades de las ecuaciones.
Aplicaciones de la factorización
La factorización tiene múltiples aplicaciones en diversas áreas de las matemáticas y la ciencia, como:
- Resolución de ecuaciones cuadráticas: La factorización es una de las técnicas principales para resolver ecuaciones de segundo grado.
- Simplificación de fracciones algebraicas: La factorización permite simplificar fracciones complejas y realizar operaciones con ellas.
- Estudio de funciones polinomiales: La factorización ayuda a entender el comportamiento y las propiedades de las funciones polinomiales.
¿Cómo se resuelve una ecuación de 2do grado?
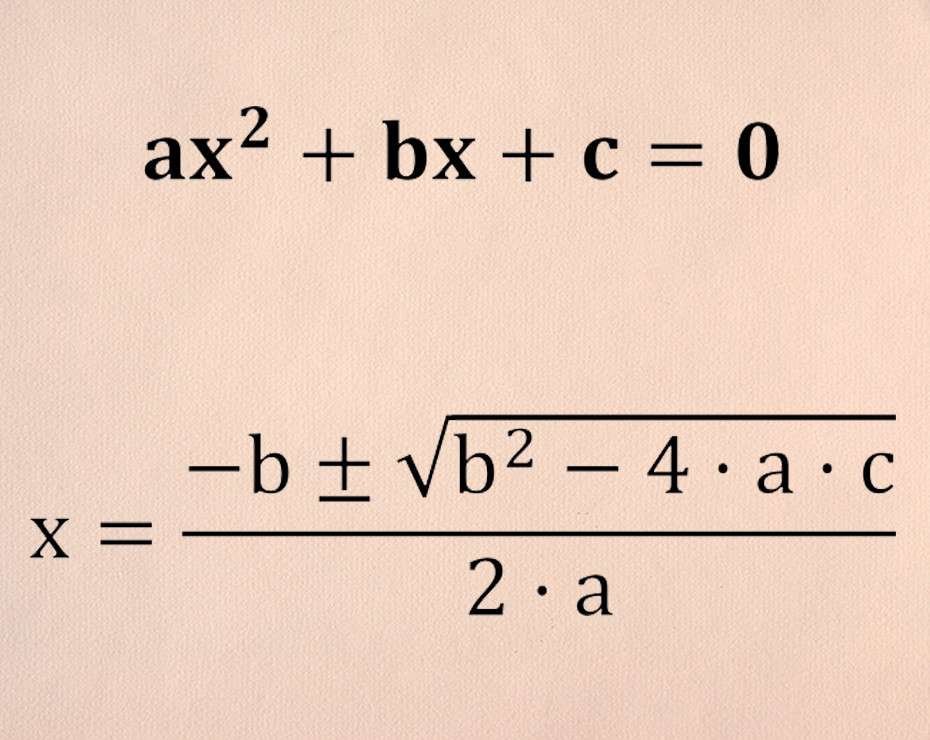
Una ecuación de segundo grado, también conocida como ecuación cuadrática, tiene la forma general ax^2 + bx + c = 0, donde a, b y c son coeficientes y a ≠ 0. Resolver una ecuación de segundo grado implica encontrar los valores de x que satisfacen la ecuación.
Método de factorización
Este método consiste en factorizar la ecuación cuadrática en dos binomios. Si los binomios son iguales a cero, entonces cualquiera de ellos puede ser una solución.
- Factorizar la ecuación cuadrática.
- Igualar cada factor a cero.
- Resolver las ecuaciones lineales resultantes.
Utilizando la fórmula cuadrática
La fórmula cuadrática es una herramienta poderosa para resolver ecuaciones de segundo grado. Esta fórmula es: x = [-b ± √(b^2 – 4ac)] / (2a)
- Identificar los coeficientes a, b y c en la ecuación cuadrática.
- Sustituir estos valores en la fórmula cuadrática.
- Calcular el valor de los dos posibles resultados para x.
Completando el cuadrado
Este método implica manipular la ecuación cuadrática para que uno de sus lados se convierta en un trinomio cuadrado perfecto.
- Mover el término constante al otro lado de la ecuación.
- Agregar el término necesario para completar el cuadrado en ambos lados.
- Factorizar el cuadrado perfecto y resolver para x.
Preguntas Frecuentes
¿Qué es una ecuación de segundo grado?
Una ecuación de segundo grado es una ecuación cuadrática que presenta la forma general ax^2 + bx + c = 0, donde a, b y c son números reales y a es distinto de cero. Estas ecuaciones son de gran importancia en diversas áreas de la matemática y otras disciplinas científicas, ya que permiten modelar una amplia variedad de situaciones reales. Su solución puede obtenerse mediante diferentes métodos, siendo uno popular la factorización.
¿Cómo se resuelve una ecuación de segundo grado por factorización?
Para resolver una ecuación de segundo grado por factorización, primero se deben identificar los términos a, b y c de la ecuación cuadrática. Luego, se busca dos números que multiplicados den ac y sumados den b. Estos números se utilizan para descomponer la ecuación en dos binomios. Finalmente, se iguala cada binomio a cero y se resuelve para x, obteniendo así las raíces de la ecuación.
¿Cuándo una ecuación de segundo grado no puede resolverse por factorización?
Una ecuación de segundo grado no puede resolverse por factorización cuando no existen dos números que multiplicados den ac y sumados den b. Esto suele ocurrir cuando la ecuación tiene raíces complejas o irracionales. En estos casos, se deben emplear otros métodos de resolución, como la fórmula general o el método de completar el cuadrado.
¿Cuáles son los pasos para factorizar una ecuación de segundo grado?
Para factorizar una ecuación de segundo grado, se siguen los siguientes pasos: Primero, identifica los términos a, b y c de la ecuación. Luego, busca dos números que multiplicados den ac y sumados den b. A continuación, reescribe la ecuación reemplazando bx por la suma de los dos números encontrados. Después, factoriza por agrupación, dividiendo la ecuación en dos grupos y factorizando cada uno. Finalmente, factoriza nuevamente para obtener la forma (ax + m)(ax + n) = 0, donde m y n son los números encontrados.


Deja una respuesta