Contenido
El cálculo del área de un triángulo es una habilidad fundamental en geometría y matemáticas.
Aunque pueda parecer complejo a primera vista, es un proceso bastante sencillo una vez que se entienden los principios básicos. Este artículo te proporcionará una guía paso a paso para calcular el área de cualquier triángulo, independientemente de su forma o tamaño. Además, te ofreceremos ejemplos prácticos y consejos útiles para ayudarte a comprender y dominar este concepto esencial. Así que, si estás listo para desmitificar el cálculo del área de un triángulo, ¡empecemos!
Cómo Calcular el Área de un Triángulo: Guía Paso a Paso
El cálculo del área de un triángulo es una de las habilidades fundamentales en geometría. Aunque existen varias fórmulas para calcular el área de un triángulo, dependiendo de la información que tengas disponible, la fórmula más común es

Donde:
- es el área del triángulo.
- es la longitud de la base del triángulo.
- es la altura del triángulo (la perpendicular trazada desde la base hasta el vértice opuesto).
A continuación, te guío paso a paso para calcular el área de un triángulo.
Paso 1: Identifica la base y la altura del triángulo
La base de un triángulo puede ser cualquier uno de sus lados, pero generalmente se elige el lado horizontal. La altura es la distancia perpendicular de la base al vértice opuesto. Es importante recordar que la altura debe ser perpendicular a la base.
Paso 2: Mide la base y la altura
Una vez que hayas identificado la base y la altura del triángulo, es necesario medirlas. Puedes usar una regla o una cinta métrica para obtener estas medidas. Asegúrate de que las medidas estén en las mismas unidades (por ejemplo, centímetros, metros, pulgadas, etc.).
Paso 3: Aplica la fórmula del área del triángulo
La fórmula para calcular el área de un triángulo es: Área = (base altura) / 2
Paso 4: Sustituye los valores en la fórmula
Una vez que tengas las medidas de la base y la altura, sustitúyelas en la fórmula. Por ejemplo, si la base mide 6 cm y la altura mide 4 cm, la fórmula sería: Área = (6 4) / 2
Paso 5: Calcula el área
Finalmente, realiza las operaciones matemáticas. En el ejemplo anterior, el cálculo sería: Área = (6 4) / 2 = 24 / 2 = 12 cm² Por lo tanto, el área del triángulo es de 12 cm².
| Paso | Descripción | Fórmula/Ejemplo |
|---|---|---|
| Paso 1 | Identificar la base y la altura | Base: lado horizontal, Altura: perpendicular a la base |
| Paso 2 | Medir la base y la altura | Usar una regla o cinta métrica |
| Paso 3 | Aplicar la fórmula del área | Área = (base altura) / 2 |
| Paso 4 | Sustituir valores en la fórmula | Ejemplo: Área = (6 4) / 2 |
| Paso 5 | Calcular el área | Resultado del ejemplo: 12 cm² |
¿Cómo sacar el área de un triángulo paso a paso?

Fórmula para calcular el área de un triángulo
El área de un triángulo se calcula utilizando la fórmula: A = (base altura) / 2. Donde A es el área, base es el largo de uno de los lados del triángulo y altura es la distancia perpendicular desde el lado opuesto hasta el vértice opuesto.
- Identificar la base y la altura del triángulo.
- Multiplicar la base por la altura.
- Dividir el resultado por 2 para obtener el área.
Tipos de triángulos y su área
Existen diferentes tipos de triángulos, pero la fórmula para calcular el área es la misma para todos. Sin embargo, la forma de obtener la base y la altura puede variar dependiendo del tipo de triángulo.
- Triángulo equilátero: Todos los lados y ángulos son iguales. La altura se puede calcular utilizando la fórmula: h = (sqrt(3) a) / 2, donde a es el lado del triángulo.
- Triángulo isósceles: Dos lados y dos ángulos son iguales. La altura se puede calcular utilizando la fórmula: h = sqrt(a^2 – (b^2 / 4)), donde a es el lado desigual y b es la base.
- Triángulo escaleno: Todos los lados y ángulos son diferentes. La altura se debe obtener mediante la perpendicular desde el vértice opuesto a la base.
Consejos para calcular el área de un triángulo
Para calcular el área de un triángulo de manera precisa, es importante tener en cuenta los siguientes consejos:
- Asegurarse de tener las medidas correctas de la base y la altura.
- Verificar que la altura sea perpendicular a la base.
- Utilizar una calculadora para realizar los cálculos, especialmente si se trata de números decimales o fracciones.
¿Cuántas formas hay para calcular el área de un triángulo?
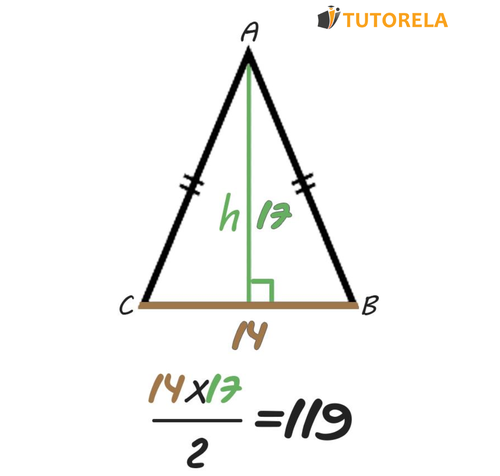
Existen varias formas de calcular el área de un triángulo, dependiendo de la información que se tenga disponible. A continuación, se presentan tres métodos comunes:
Fórmula básica: base y altura
La forma más conocida para calcular el área de un triángulo es utilizando la fórmula Área = (base altura) / 2. Esta fórmula requiere conocer la longitud de la base del triángulo y la altura perpendicular a esa base.
- Identificar la base y la altura del triángulo.
- Multiplicar la base por la altura.
- Dividir el resultado por 2 para obtener el área.
Teorema de Pitágoras
Cuando se conocen las longitudes de los tres lados del triángulo, se puede utilizar el teorema de Pitágoras para calcular el área. Este método es especialmente útil para triángulos rectángulos.
- Calcular la longitud de la altura utilizando el teorema de Pitágoras: altura² + cateto² = hipotenusa².
- Una vez obtenida la altura, utilizar la fórmula básica del área: (base altura) / 2.
Fórmula de Herón
La fórmula de Herón permite calcular el área de un triángulo cuando se conocen las longitudes de los tres lados (a, b y c). Esta fórmula es

, donde s es el semiperímetro del triángulo (a + b + c) / 2.
- Calcular el semiperímetro del triángulo: s = (a + b + c) / 2.
- Aplicar la fórmula de Herón: Área = √(s (s – a) (s – b) (s – c)).
¿Cómo se saca el área de un triángulo rectángulo?

Para calcular el área de un triángulo rectángulo, se utiliza la fórmula:
Área = (base altura) / 2
Donde la base es uno de los lados que forman el ángulo recto y la altura es la distancia perpendicular desde la base hasta el vértice opuesto.
Pasos para calcular el área de un triángulo rectángulo
- Identifica la base y la altura del triángulo rectángulo.
- Multiplica la base por la altura.
- Divide el resultado de la multiplicación entre 2 para obtener el área.
Propiedades del triángulo rectángulo
- Un triángulo rectángulo tiene un ángulo de 90 grados.
- Los catetos son los dos lados que forman el ángulo recto.
- La hipotenusa es el lado opuesto al ángulo recto y es el lado más largo del triángulo.
Aplicaciones prácticas
- La fórmula del área de un triángulo rectángulo se utiliza en diversas áreas, como la arquitectura, la ingeniería y la física.
- Permite calcular el área de superficies que tengan forma de triángulo rectángulo, como terrenos, construcciones o piezas mecánicas.
- Es fundamental para resolver problemas geométricos y trigonométricos que involucren triángulos rectángulos.
¿Cuál es la fórmula para calcular triángulos?

Fórmula para calcular el área de un triángulo
El área de un triángulo se calcula utilizando la fórmula A = (base altura) / 2. La base es el lado sobre el cual se mide la altura, y la altura es la distancia perpendicular desde la base hasta el vértice opuesto. Aquí te menciono los pasos para calcular el área:
- Identifica la base y la altura del triángulo.
- Multiplica la base por la altura.
- Divide el resultado de la multiplicación entre 2.
Fórmula para calcular el perímetro de un triángulo
El perímetro de un triángulo es la suma de la longitud de todos sus lados. Para calcularlo, simplemente se suman los tres lados:
- Identifica las longitudes de los tres lados del triángulo.
- Suma las longitudes de los tres lados.
Teorema de Pitágoras para triángulos rectángulos
El Teorema de Pitágoras se utiliza específicamente para calcular la longitud de uno de los lados de un triángulo rectángulo, siempre y cuando se conozcan las longitudes de los otros dos lados. La fórmula es a² + b² = c², donde c es la longitud de la hipotenusa (el lado más largo), y a y b son las longitudes de los otros dos lados (catetos).
- Identifica las longitudes de los dos catetos (a y b) o de un cateto y la hipotenusa (c).
- Si conoces los catetos, suma el cuadrado de sus longitudes para obtener el cuadrado de la hipotenusa.
- Si conoces la hipotenusa y un cateto, resta el cuadrado del cateto del cuadrado de la hipotenusa para obtener el cuadrado del otro cateto.
- Obtén la longitud desconocida al calcular la raíz cuadrada del resultado.
Preguntas Frecuentes
¿Cuál es la fórmula para calcular el área de un triángulo?
La fórmula para calcular el área de un triángulo es (base altura) / 2. Esta es una de las fórmulas matemáticas más básicas y esenciales que debes conocer. La base se refiere a la longitud de uno de los lados del triángulo, mientras que la altura es la distancia perpendicular desde la base hasta el vértice opuesto.
¿Cómo se diferencia la base de la altura en un triángulo?
La base de un triángulo puede ser cualquiera de sus tres lados, pero una vez elegida, la altura debe ser la distancia perpendicular desde ese lado hasta el vértice opuesto. La altura siempre forma un ángulo recto (90 grados) con la base. La elección de la base puede depender del problema específico que estés resolviendo y de la información que tengas disponible.
¿Qué es la altura de un triángulo y cómo se mide?
La altura de un triángulo es la distancia perpendicular desde un vértice del triángulo hasta la base o su extensión. Para medir la altura, se traza una línea perpendicular desde el vértice opuesto a la base hasta el punto donde se intersecta con la base. La longitud de esta línea es la altura del triángulo. Es importante tener en cuenta que, dependiendo del triángulo, la altura puede caer dentro o fuera de este.
¿Puede la altura de un triángulo ser mayor que la longitud de la base?
Sí, la altura de un triángulo puede ser mayor que la longitud de la base, especialmente en el caso de triángulos obtusángulos. En un triángulo obtusángulo, uno de los ángulos es mayor de 90 grados, lo que puede hacer que la altura desde ese ángulo hasta la base sea más larga que la propia base. Sin embargo, en un triángulo rectángulo, la altura siempre será igual o menor que la longitud de la base.


Deja una respuesta