Contenido
El rombo, una figura geométrica fascinante, es un polígono de cuatro lados iguales que a menudo despierta interés tanto en estudiantes como en profesionales del ámbito matemático. En este artículo, exploraremos la fórmula para calcular el área de un rombo y resolveremos algunos ejemplos prácticos para facilitar su comprensión.
La fórmula del área del rombo puede resultar un tanto compleja para aquellos que se acercan a ella por primera vez, pero con los ejemplos adecuados y una explicación detallada, descubriremos que no solo es manejable, sino también bastante interesante.
Área de un Rombo: Fórmula y Ejemplos Resueltos
El rombo es un tipo especial de paralelogramo, caracterizado por tener todos sus lados de igual longitud. El cálculo del área de un rombo puede ser realizado mediante varias fórmulas, dependiendo de los datos proporcionados. A continuación, estudiaremos la fórmula básica y ejemplos resueltos para comprender mejor este concepto.
Fórmula para calcular el área de un rombo
La fórmula principal para calcular el área de un rombo es:
Área = (Diagonal Mayor Diagonal Menor) / 2 Donde: – Diagonal Mayor (D1) es la longitud de la diagonal más larga del rombo. – Diagonal Menor (D2) es la longitud de la diagonal más corta del rombo.
Ejemplo 1: Calculando el área conociendo las diagonales
Supongamos que tenemos un rombo con diagonales de longitudes 8 cm y 6 cm. Para calcular el área, utilizamos la fórmula: Área = (D1 D2) / 2 Área = (8 cm 6 cm) / 2 Área = 48 cm² / 2 Área = 24 cm²
| Datos | Resultados |
|---|---|
| Diagonal Mayor (D1) = 8 cm | Área = 24 cm² |
| Diagonal Menor (D2) = 6 cm |
Relación entre el área del rombo y la del rectángulo
El área de un rombo puede ser entendida también como el área de un rectángulo que tiene las mismas dimensiones que las diagonales del rombo. Esto se debe a que las diagonales de un rombo se cruzan en un ángulo recto, dividiendo al rombo en cuatro triángulos rectángulos congruentes.
Aplicaciones prácticas del cálculo del área de un rombo
El cálculo del área de un rombo es útil en diversas situaciones prácticas, como en la arquitectura, diseño gráfico, ingeniería y carpintería. Comprender cómo calcular el área correctamente permite realizar planificaciones y cálculos precisos en proyectos que involucran formas geométricas.
¿Cómo es la fórmula del área de un rombo?
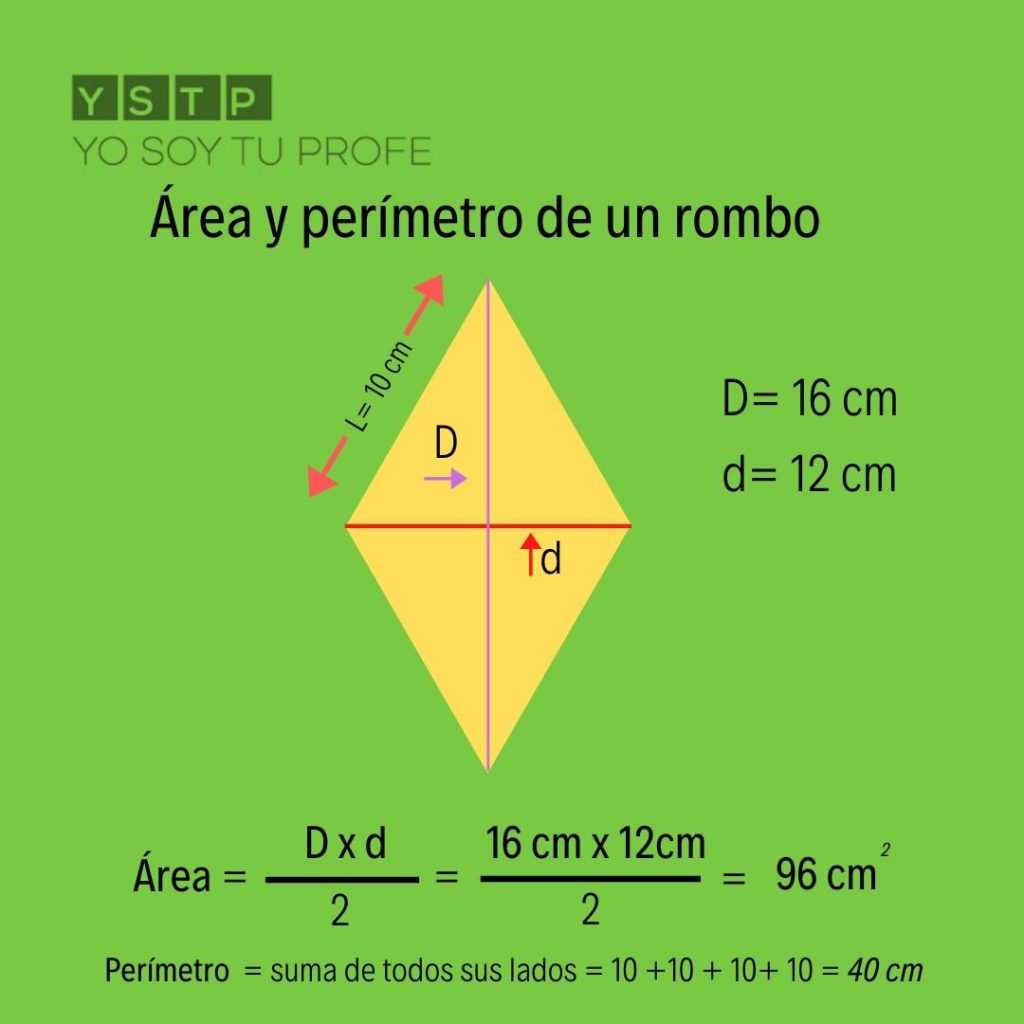
La fórmula del área de un rombo se calcula multiplicando la longitud de las diagonales y dividiendo el resultado por 2. Es decir, el área de un rombo es igual a (diagonal mayor diagonal menor) / 2.
¿Cuáles son las diagonales de un rombo?
Las diagonales de un rombo son las rectas que unen dos vértices opuestos del rombo. Estas se intersectan en el centro del rombo formando un ángulo de 90 grados. Todas las figuras con forma de rombo tienen dos diagonales.
- Diagonal mayor: Es la recta más larga que une dos vértices opuestos del rombo.
- Diagonal menor: Es la recta más corta que une los otros dos vértices opuestos del rombo.
- Propiedad de las diagonales: Las diagonales de un rombo son perpendiculares entre sí y se bisecan (cortan en dos partes iguales) una a la otra.
¿Cómo se aplica la fórmula del área de un rombo?
Para calcular el área de un rombo, primero debes conocer la longitud de ambas diagonales. Una vez que las tengas, simplemente multiplica la diagonal mayor por la diagonal menor y divide el resultado por 2.
- Paso 1: Identifica la longitud de la diagonal mayor y la diagonal menor del rombo.
- Paso 2: Multiplica la longitud de la diagonal mayor por la longitud de la diagonal menor.
- Paso 3: Divide el resultado obtenido en el paso 2 por 2. Este será el área del rombo.
¿Cómo se puede comprobar la fórmula del área de un rombo?
La fórmula del área de un rombo se puede comprobar utilizando la propiedad de que las diagonales de un rombo lo dividen en cuatro triángulos congruentes. Al calcular el área de uno de estos triángulos y multiplicarlo por 4, se obtiene el área total del rombo, lo cual coincide con la fórmula mencionada.
- Triángulos congruentes: Al trazar las diagonales de un rombo, este se divide en cuatro triángulos congruentes (iguales en forma y tamaño).
- Área de un triángulo: El área de un triángulo se calcula multiplicando la base por la altura y dividiendo por 2.
- Comprobación: Sumando el área de los cuatro triángulos se obtiene el área total del rombo, lo cual es igual a (diagonal mayor diagonal menor) / 2.
¿Cómo se lee el área del rombo?
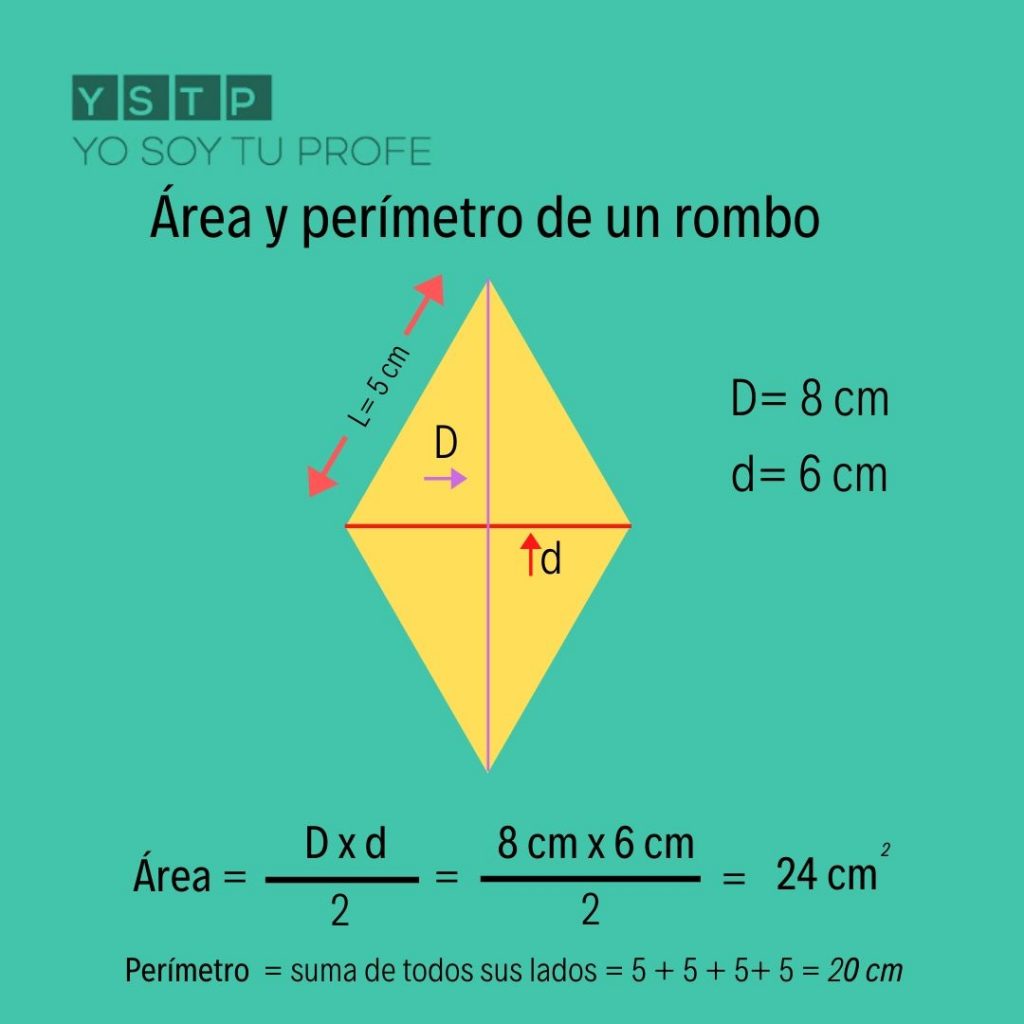
El área del rombo se lee multiplicando la longitud de sus diagonales y dividiendo el resultado por 2. Es decir, si D1 y D2 son las longitudes de las diagonales del rombo, entonces el área (A) se calcula mediante la fórmula: A = (D1 D2) / 2.
Fórmula para calcular el área del rombo
El área de un rombo se calcula utilizando la siguiente fórmula:
- Identificar las diagonales del rombo, que son las dos líneas que se cruzan en el centro del rombo formando ángulos rectos.
- Medir la longitud de cada diagonal y anotar sus valores como D1 y D2.
- Multiplicar las longitudes de las diagonales (D1 D2) y dividir el resultado por 2. Este es el área del rombo.
Características del rombo
Un rombo tiene varias características distintivas:
- Es un cuadrilátero de lados iguales.
- Sus diagonales se cortan en ángulos rectos y se dividen en segmentos de igual longitud.
- Los ángulos opuestos del rombo son iguales.
Aplicaciones prácticas del cálculo del área del rombo
Calcular el área de un rombo es útil en muchas situaciones prácticas:
- En diseño gráfico, para determinar el espacio que ocupará una imagen o diseño con forma de rombo en una página.
- En arquitectura y construcción, para calcular el área de superficies con forma de rombo, como ventanas o suelos.
- En geomorfología, para calcular el área de formaciones naturales con forma de rombo.
¿Cuál es el perímetro del rombo?

Para calcular el perímetro de un rombo, es necesario conocer la longitud de uno de sus lados, ya que todos los lados de un rombo tienen la misma medida. El perímetro se calcula sumando la longitud de los cuatro lados. Si llamamos L a la longitud de uno de los lados del rombo, la fórmula para calcular el perímetro (P) es:
P = 4L
Propiedades del rombo relacionadas con su perímetro
El rombo tiene varias propiedades que lo caracterizan y que están relacionadas con su perímetro. Algunas de estas propiedades son:
- Todos los lados del rombo son iguales, lo que facilita el cálculo del perímetro.
- Las diagonales del rombo se cortan en ángulo recto y dividen al rombo en cuatro triángulos congruentes.
- El perímetro del rombo no se ve afectado por la medida de sus ángulos, sino solo por la longitud de sus lados.
Cómo medir los lados de un rombo
Para poder calcular el perímetro de un rombo, es necesario conocer la longitud de uno de sus lados. Esto se puede hacer de varias maneras:
- Usando una regla o un calibrador, medir directamente la longitud de uno de los lados.
- Si se conocen las coordenadas de los vértices del rombo, se puede calcular la distancia entre dos vértices adyacentes usando el teorema de Pitágoras.
- Si se conocen las longitudes de las diagonales del rombo, se puede calcular la longitud de un lado usando el teorema de Pitágoras, ya que cada diagonal divide al rombo en dos triángulos rectángulos.
Ejemplo de cálculo del perímetro de un rombo
Supongamos que tenemos un rombo cuya longitud de un lado es de 5 cm. Para calcular su perímetro, simplemente multiplicamos la longitud del lado por 4:
P = 4L
P = 4 5 cm
P = 20 cm
Por lo tanto, el perímetro de este rombo es de 20 cm.
¿Cuál es la fórmula para calcular el área de un romboide?
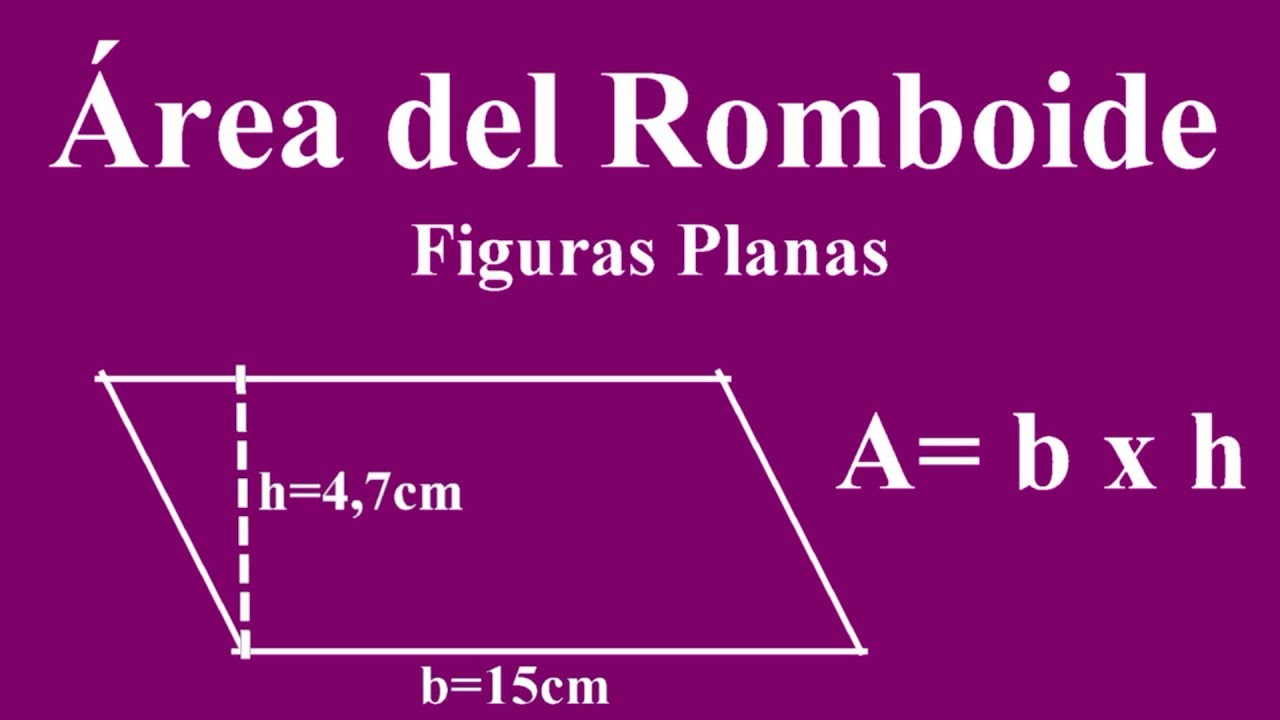
La fórmula para calcular el área de un romboide es la siguiente:
Área = base × altura
Donde la base es el largo de uno de los lados del romboide, y la altura es la distancia perpendicular desde la base hasta el lado opuesto.
Definición de romboide
Un romboide es un paralelogramo cuyos ángulos no son rectos y cuyos lados no son todos iguales. Es un cuadrilátero con dos pares de lados paralelos.
Cómo medir la base y la altura de un romboide
- La base es uno de los lados del romboide. Puedes elegir cualquier lado como base.
- La altura es la distancia perpendicular desde la base hasta el lado opuesto. Esta distancia debe medirse en un ángulo recto con respecto a la base.
- Puedes utilizar una regla para medir la longitud de la base y la altura. Asegúrate de que la regla esté alineada correctamente cuando midas la altura.
Ejemplo de cálculo del área de un romboide
Supongamos que tenemos un romboide con una base de 10 cm y una altura de 5 cm. Para calcular el área, simplemente multiplicamos la base por la altura:
Área = base × altura = 10 cm × 5 cm = 50 cm²
Por lo tanto, el área del romboide es 50 cm².
Preguntas Frecuentes
¿Cuál es la fórmula para calcular el área de un rombo?
La fórmula para calcular el área de un rombo es: A = (D d) / 2, donde D representa la longitud de la diagonal mayor, y d representa la longitud de la diagonal menor. Esta fórmula se deriva del hecho de que un rombo se puede dividir en cuatro triángulos rectángulos iguales por sus diagonales.
¿Cómo se pueden calcular las diagonales de un rombo?
Para calcular las diagonales de un rombo, se puede utilizar la fórmula: D = 2 A / d y d = 2 A / D, donde A es el área del rombo, D es la diagonal mayor y d es la diagonal menor. Estas fórmulas se pueden deducir directamente de la fórmula del área del rombo.
¿Pueden las diagonales de un rombo ser iguales?
Sí, en el caso particular de un cuadrado, que es un tipo especial de rombo, las diagonales son iguales. Sin embargo, en un rombo general, las diagonales pueden ser de longitudes diferentes. Las diagonales de un rombo siempre se cruzan en un ángulo de 90 grados y se bisecan (dividen por la mitad) mutuamente, independientemente de sus longitudes.
¿Cómo se puede utilizar la fórmula del área de un rombo en problemas prácticos?
La fórmula del área de un rombo se puede utilizar en una variedad de problemas prácticos, especialmente en aquellos que implican medidas y cálculos de superficies. Por ejemplo, si se necesita calcular el área de un terreno con forma de rombo, se pueden medir las longitudes de las diagonales y luego aplicar la fórmula A = (D d) / 2 para obtener el área. Esta información puede ser útil para planificar la construcción, la agricultura, entre otras aplicaciones.


Deja una respuesta